向量的基本运算

　

向量运算

向量是什么

向量就是给定一个点A，连接原点到点A，并具有由O到A方向的连线，表示为$\overrightarrow{OA}$OA. 书本的定义：向量就是具有大小和方向东西。

大小(magnitude)

向量的大小(magnitude)写作$\mathrm{\parallel }x\mathrm{\parallel }$∥x∥,称为模(norm).

通过（Pythagoras’ theorem）毕达哥拉斯定理求模如下图，

${OA}^2={OB}^2+{AB}^2$OA2=OB2+AB2

${OA}^2=3^2+4^2$OA2=32+42

$\mathrm{\parallel }x\mathrm{\parallel }=5$∥x∥=5

方向（direction）

定义向量$\mathbf{u}(u_1,u_2)$u(u1​,u2​)的方向为向量$\mathbf{w}(\frac{u_1}{\mathrm{\parallel }u\mathrm{\parallel }},\frac{u_2}{\mathrm{\parallel }u\mathrm{\parallel }})$w(∥u∥u1​​,∥u∥u2​​)。如下图：

可以看到：

$cos\left(\theta \right)=\frac{u_1}{\mathrm{\parallel }u\mathrm{\parallel }}$cos(θ)=∥u∥u1​​

$cos\left(\alpha \right)=\frac{u_2}{\mathrm{\parallel }u\mathrm{\parallel }}$cos(α)=∥u∥u2​​

所以向量$\mathbf{u}(3,4)$u(3,4)方向向量是$\mathbf{w}(0.6,0.8)$w(0.6,0.8)。方向向量的模为1.如下图

两个向量的加法

任意给给两个向量$\mathbf{u}(u_1,u_2)$u(u1​,u2​) ，$\mathbf{v}(v_1,v_2)$v(v1​,v2​)两个向量相加：$\mathbf{u}+\mathbf{v}=(u_1+v_1,u_2+v_2)$u+v=(u1​+v1​,u2​+v2​)


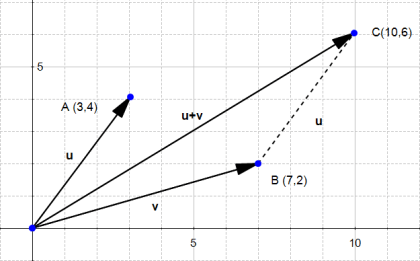
两个向量的减法

任意给给两个向量$\mathbf{u}(u_1,u_2)$u(u1​,u2​) ，$\mathbf{v}(v_1,v_2)$v(v1​,v2​)两个向量相减：$\mathbf{u}-\mathbf{v}=(u_1-v_1,u_2-v_2)$u−v=(u1​−v1​,u2​−v2​)。 方向指向被减数的方向。

向量的点积（dot product）

$\mathbf{x}\cdot \mathbf{y}=\mathrm{\parallel }x\mathrm{\parallel }\mathrm{\parallel }y\mathrm{\parallel }cos\left(\theta \right)$x⋅y=∥x∥∥y∥cos(θ), $\theta$θ 为两个向量的夹角。

推导过程如下：

根据前面的分析我们知道，

$cos\left(\beta \right)=\frac{adjacent}{hypotenuse}=\frac{x_1}{\mathrm{\parallel }x\mathrm{\parallel }}$cos(β)=hypotenuseadjacent​=∥x∥x1​​

$sin\left(\beta \right)=\frac{opposite}{hypotenuse}=\frac{x_2}{\mathrm{\parallel }x\mathrm{\parallel }}$sin(β)=hypotenuseopposite​=∥x∥x2​​

$cos\left(\alpha \right)=\frac{adjacent}{hypotenuse}=\frac{y_1}{\mathrm{\parallel }y\mathrm{\parallel }}$cos(α)=hypotenuseadjacent​=∥y∥y1​​

$sin\left(\alpha \right)=\frac{opposite}{hypotenuse}=\frac{y_2}{\mathrm{\parallel }y\mathrm{\parallel }}$sin(α)=hypotenuseopposite​=∥y∥y2​​

从图片中得到 $\theta =\beta -\alpha$θ=β−α, 那么$cos\left(\theta \right)=cos(\beta -\alpha )$cos(θ)=cos(β−α)

$cos(\beta -\alpha )=cos\left(\beta \right)cos\left(\alpha \right)+sin\left(\beta \right)sin\left(\alpha \right)$cos(β−α)=cos(β)cos(α)+sin(β)sin(α)

于是，

$cos\left(\theta \right)=cos(\beta -\alpha )=cos\left(\beta \right)cos\left(\alpha \right)+sin\left(\beta \right)sin\left(\alpha \right)$cos(θ)=cos(β−α)=cos(β)cos(α)+sin(β)sin(α)

$cos\left(\theta \right)=\frac{x_1}{\mathrm{\parallel }x\mathrm{\parallel }}\frac{y_1}{\mathrm{\parallel }y\mathrm{\parallel }}+\frac{x_2}{\mathrm{\parallel }x\mathrm{\parallel }}\frac{y_2}{\mathrm{\parallel }y\mathrm{\parallel }}$cos(θ)=∥x∥x1​​∥y∥y1​​+∥x∥x2​​∥y∥y2​​

$cos\left(\theta \right)=\frac{x_1{y}_1+x_2{y}_2}{\mathrm{\parallel }x\mathrm{\parallel }\mathrm{\parallel }y\mathrm{\parallel }}$cos(θ)=∥x∥∥y∥x1​y1​+x2​y2​​

$\mathrm{\parallel }x\mathrm{\parallel }\mathrm{\parallel }y\mathrm{\parallel }cos\left(\theta \right)=x_1{y}_1+x_2{y}_2$∥x∥∥y∥cos(θ)=x1​y1​+x2​y2​

点积的算术定义就出来，

$\mathbf{x}\cdot \mathbf{y}=x_1{y}_1+x_2{y}_2=\sum _{i=1}^2\left(x_i{y}_i\right)$x⋅y=x1​y1​+x2​y2​=i=1∑2​(xi​yi​)

从上面的集合定义也能知道，两个向量的点积是一个数。

向量的正交投影

如图给定两个向量x，y，那么向量x在y上的投影为z。

通过上面的学习我们知道，

$cos\left(\theta \right)=\frac{\mathrm{\parallel }z\mathrm{\parallel }}{\mathrm{\parallel }x\mathrm{\parallel }}$cos(θ)=∥x∥∥z∥​

$\mathrm{\parallel }z\mathrm{\parallel }=\mathrm{\parallel }x\mathrm{\parallel }cos\left(\theta \right)$∥z∥=∥x∥cos(θ)

点积$cos\left(\theta \right)=\frac{\mathbf{x}\cdot \mathbf{y}}{\mathrm{\parallel }x\mathrm{\parallel }\mathrm{\parallel }y\mathrm{\parallel }}$cos(θ)=∥x∥∥y∥x⋅y​

于是可以推导得

$\mathrm{\parallel }z\mathrm{\parallel }=\frac{\mathbf{x}\cdot \mathbf{y}}{\mathrm{\parallel }y\mathrm{\parallel }}$∥z∥=∥y∥x⋅y​

另外我们知道方向向量的，如果u表示向量y的方向向量，$\mathbf{u}=\frac{\mathbf{y}}{\mathrm{\parallel }y\mathrm{\parallel }}$u=∥y∥y​, 那么向量x在向量y上面的投影可以由下式计算：

$\mathrm{\parallel }z\mathrm{\parallel }=\mathbf{u}\cdot \mathbf{x}$∥z∥=u⋅x

我们还注意到，向量x在向量y上的投影得到的向量z，它的方向向量和向量y的方向向量是一致的，所以向量z可表示为$\mathbf{z}=\mathrm{\parallel }z\mathrm{\parallel }\mathbf{u}$z=∥z∥u。

知道了向量x在向量y上面的投影z后，我们就能够计算向量x-z的距离:

$\mathrm{\parallel }x-z\mathrm{\parallel }=\sqrt{(3-4{)}^2+(5-1{)}^2}=\sqrt{17}$∥x−z∥=(3−4)2+(5−1)2​=17​

详见原文地址：https://www.svm-tutorial.com/2014/11/svm-understanding-math-part-2/

相关阅读

SVM支持向量机原理及核函数

原文链接：SVM支持向量机原理及核函数 转载请注明出处 支持向量机原理 大距离分类算法 1、名词解释： 分割超平面：如下图所示，构造

向量点乘相关公式推导

1.向量点乘公式推导和几何解释一般来说，点乘结果描述了两个向量的“相似”程度，点乘结果越大，两向量越相近。01.向量点乘(dot produc

复数计算和向量计算的区别

今天接触到了量子计算，原理正在摸索，但是从数学角度，复数计算应该会用到。 以前学习复数的时候，纯属应付考试，现在回想只记得一个公式：，

法向半球内单位向量(切空间) 转世界空间表示

已知此切线空间的法线在世界空间中的表示N，求此切线空间构成的半球形空间任意单位向量(θ，φ)在世界空间中的表示 首先根据N,计算该

AI产品经理必懂算法：支持向量机SVM

作为AI产品经理必懂算法的第二篇，来了解一下支持向量机SVM算法，英文全称是“Support Vector Machine”。在机器学习中，SVM是监督学习