attention各种形式总结

　

attention

attention 总结

参考：注意力机制（Attention Mechanism）在自然语言处理中的应用

Attention函数的本质可以被描述为一个查询（query）到一系列（键key-值value）对的映射，如下图。

在计算attention时主要分为三步:

• 第一步是将query和每个key进行相似度计算得到权重，常用的相似度函数有点积，拼接，感知机等；
• 第二步一般是使用一个softmax函数对这些权重进行归一化；
• 最后将权重和相应的键值value进行加权求和得到最后的attention。
• 目前在NLP研究中，key和value常常都是同一个，即key=value。

• 

• Attention在NLP中其实我觉得可以看成是一种自动加权，它可以把两个你想要联系起来的不同模块，通过加权的形式进行联系。目前主流的计算公式有以下几种：

  

  通过设计一个函数将目标模块mt和源模块ms联系起来，然后通过一个soft函数将其归一化得到概率分布。

• 目前Attention在NLP中已经有广泛的应用。它有一个很大的优点就是可以可视化attention矩阵来告诉大家神经网络在进行任务时关注了哪些部分。不过在NLP中的attention机制和人类的attention机制还是有所区别，它基本还是需要计算所有要处理的对象，并额外用一个矩阵去存储其权重，其实增加了开销。而不是像人类一样可以忽略不想关注的部分，只去处理关注的部分。

一、传统encoder-decoder模型

encoder-decoder模型

也就是编码-解码模型。所谓编码，就是将输入序列转化成一个固定长度的向量；解码，就是将之前生成的固定向量再转化成输出序列。

具体实现的时候，编码器和解码器都不是固定的,可选的有CNN/RNN/BiRNN/GRU/LSTM等等，你可以自由组合。比如说，你在编码时使用BiRNN,解码时使用RNN，或者在编码时使用RNN,解码时使用LSTM等等。

1.1 encoder

• 对于输入序列x=(x1,...,xTx)" role="presentation" style="position: relative;">x=(x1,...,xTx)$x=(x_1,...,x_{T_x})$,其会将输入序列如图所示编码成一个context vector c ，encoder一般使用RNN，在RNN中，当前时间的隐藏状态是由上一时间的状态和当前时间输入决定的，也就是
  ht=f(xt,ht−1)" role="presentation" style="position: relative;">ht=f(xt,ht−1)$h_t=f(x_t,h_{t-1})$
• 获得了各个时间段的隐藏层以后，再将隐藏层的信息汇总，生成最后的语义向量 c，相当于把整个句子的信息都包含了，可以看成整个句子的一个语义表示。
  c=q(ht,...,hTx)" role="presentation" style="position: relative;">c=q(ht,...,hTx)$c=q(h_t,...,h_{T_x})$

  其中的f和q是非线性的函数

  例如，在论文中有使用

  q(ht,...,hTx)=hTx" role="presentation" style="position: relative;">q(ht,...,hTx)=hTx$q(h_t,...,h_{T_x})=h_{T_x}$

  来简化计算

1.2 decoder

一般其作用为在给定context vector c和所有已预测的词{y1,...,yt−1}" role="presentation" style="position: relative;">{y1,...,yt−1}$\{y_1,...,y_{t-1}\}$去预测yt" role="presentation" style="position: relative;">yt$y_t$，故t时刻翻译的结果y为以下的联合概率分布

p(y)=∏t=1Tp(yt|{y1,...,yt},c)" role="presentation">p(y)=∏t=1Tp(yt|{y1,...,yt},c)$$p(y)=\prod _{t=1}^{T}p(y_t|\{y_1,...,y_t\},c)$$

• 在RNN中（如上图所示），t时刻隐藏状态st" role="presentation" style="position: relative;">st$s_t$为：

  st=f(st−1,yt−1,c)" role="presentation" style="position: relative;">st=f(st−1,yt−1,c)$s_t=f(s_{t-1},y_{t-1},c)$

• 而联合条件分布为：

  p(y)=∏t=1Tp(yt|{y1,...,yt},c)=q(yt−1,st,c)" role="presentation">p(y)=∏t=1Tp(yt|{y1,...,yt},c)=q(yt−1,st,c)$$p(y)=\prod _{t=1}^{T}p(y_t|\{y_1,...,y_t\},c)=q(y_{t-1},s_t,c)$$

  其中s是输出RNN中的隐藏层，C代表之前提过的语义向量，yt−1" role="presentation" style="position: relative;">yt−1$y_{t-1}$表示上个时间段的输出，反过来作为这个时间段的输入。而q则可以是一个非线性的多层的神经网络，产生词典中各个词语属于yt" role="presentation" style="position: relative;">yt$y_t$的概率。

1.3 存在问题：

• 使用传统编码器-解码器的RNN模型先用一些LSTM单元来对输入序列进行学习，编码为固定长度的向量表示；然后再用一些LSTM单元来读取这种向量表示并解码为输出序列。采用这种结构的模型在许多比较难的序列预测问题（如文本翻译）上都取得了最好的结果，因此迅速成为了目前的主流方法。

• 然而，它存在的一个问题在于：输入序列不论长短都会被编码成一个固定长度的向量表示，而解码则受限于该固定长度的向量表示。这个问题限制了模型的性能，尤其是当输入序列比较长时，模型的性能会变得很差（在文本翻译任务上表现为待翻译的原始文本长度过长时翻译质量较差）。

• “一个潜在的问题是，采用编码器-解码器结构的神经网络模型需要将输入序列中的必要信息表示为一个固定长度的向量，而当输入序列很长时则难以保留全部的必要信息（因为太多），尤其是当输入序列的长度比训练数据集中的更长时。”

二、加入attention

来自论文：

NEURAL MACHINE TRANSLATION BY jointLY LEARNING TO ALIGN AND TRANSLATE

参考博文：深度学习笔记(六)：Encoder-Decoder模型和Attention模型

  这篇论文中首次将attention用到了nlp领域，论文中提出了一个想法，目前机器翻译的瓶颈在于无论是多长的输入，大家的普遍做法都是将所有输入通过一些方法合并成一个固定长度的向量去表示这个句子，这会造成的问题是，如果句子很长，那么这样的方法去作为decoder的输入，效果并不会很好。

 

该论文提出的加入attention的模型：

  相比于之前的encoder-decoder模型，attention模型最大的区别就在于它不在要求编码器将所有输入信息都编码进一个固定长度的向量之中。相反，此时编码器需要将输入编码成一个向量的序列，而在解码的时候，每一步都会选择性的从向量序列中挑选一个子集进行进一步处理。这样，在产生每一个输出的时候，都能够做到充分利用输入序列携带的信息。而且这种方法在翻译任务中取得了非常不错的成果。

1.1 编码（encoder）

此处并没有很多特殊，使用双向LSTM，第j个隐藏状态hj→" role="presentation" style="position: relative;">hj→$h_j\to$只能携带第j个单词本身以及之前的一些信息；而如果逆序输入，则hj←" role="presentation" style="position: relative;">hj←$h_j\leftarrow$包含第j个单词及之后的一些信息。如果把这两个结合起来，hj=[hj→,hj←]" role="presentation" style="position: relative;">hj=[hj→,hj←]$h_j=[h_j\to ,h_j\leftarrow ]$就包含了第 j 个输入和前后的信息。

1.2 解码（decoder）

1.2.1 context vector c

解码过程与传统encoder-decoder模型相同，只不过context vector c变为了ci" role="presentation" style="position: relative;">ci$c_i$

其中的ci" role="presentation" style="position: relative;">ci$c_i$是对每一个输入的{x1,...,xT}" role="presentation" style="position: relative;">{x1,...,xT}$\{x_1,...,x_T\}$encoder后的隐状态进行weighted sum（如上图所示）

ci=∑j=1Txaijhij" role="presentation" style="position: relative;">ci=∑Txj=1aijhij$c_i=\sum _{j=1}^{T_x}{a}_{ij}{h}_{ij}$

aij=exp(eij)∑k=1Txexp(eik)" role="presentation" style="position: relative;">aij=exp(eij)∑Txk=1exp(eik)$a_{ij}=\frac{exp(e_{ij})}{\sum _{k=1}^{T_x}exp(e_{ik})}$

eij=a(sj−1,hi)" role="presentation" style="position: relative;">eij=a(sj−1,hi)$e_{ij}=a(s_{j-1},h_i)$

• 注：hj" role="presentation" style="position: relative;">hj$h_j$为encoder的隐状态，sj" role="presentation" style="position: relative;">sj$s_j$为decoder的隐状态

• aij" role="presentation" style="position: relative;">aij$a_{ij}$的值越高，表示第i个输出在第j个输入上分配的注意力越多，在生成第i个输出的时候受第j个输入的影响也就越大。

• eij" role="presentation" style="position: relative;">eij$e_{ij}$ ：encoder i处隐状态和decoder j-1 处的隐状态的匹配 match，此处的 alignment model a 是和其他神经网络一起去训练（即 joint learning），其反映了hj" role="presentation" style="position: relative;">hj$h_j$的重要性

1.2.2 其余部分

其余部分均与传统相同，y的联合概率分布

p(y)=∏t=1Tp(yt|{y1,...,yt},ci)=q(yt−1,st,ci)" role="presentation">p(y)=∏t=1Tp(yt|{y1,...,yt},ci)=q(yt−1,st,ci)$$p(y)=\prod _{t=1}^{T}p(y_t|\{y_1,...,y_t\},c_i)=q(y_{t-1},s_t,c_i)$$

• 在RNN中（如上图所示），t时刻隐藏状态st" role="presentation" style="position: relative;">st$s_t$为：
  st=f(st−1,yt−1,ci)" role="presentation" style="position: relative;">st=f(st−1,yt−1,ci)$s_t=f(s_{t-1},y_{t-1},c_i)$

1.3 注意力矩阵

之前已经提过，每个输出都有一个长为Tx的注意力向量，那么将这些向量合起来看，就是一个矩阵。对其进行可视化，得到如下结果

其中x轴表示待翻译的句子中的单词(英语)，y轴表示翻译以后的句子中的单词(法语)。可以看到尽管从英语到法语的过程中，有些单词的顺序发生了变化，但是attention模型仍然很好的找到了合适的位置。换句话说，就是两种语言下的单词“对齐”了。因此，也有人把注意力模型叫做对齐(alignment)模型。而且像比于用语言学实现的硬对齐，这种基于概率的软对齐更加优雅，因为能够更全面的考虑到上下文的语境。

三、attention形式总结：

论文：Show, Attend and Tell：Neural Image Caption Generation with Visual Attention

hard attention

• 记st" role="presentation" style="position: relative;">st$s_t$ 为decoder第 t 个时刻的attention所关注的位置编号
• sti" role="presentation" style="position: relative;">sti$s_{ti}$ 表示第 t 时刻 attention 是否关注位置 i
• sti" role="presentation" style="position: relative;">sti$s_{ti}$服从多元伯努利分布(multinoulli distribution)， 对于任意的 t , sti,i=1,2,...,L" role="presentation" style="position: relative;">sti,i=1,2,...,L$s_{ti},i=1,2,...,L$中有且只有取1，其余全部为0，所以[st1,st2,...,stL]" role="presentation" style="position: relative;">[st1,st2,...,stL]$[s_{t1},s_{t2},...,s_{tL}]$是one-hot形式。
• 存在问题：hard attention不可微分，需要更加复杂的处理，在论文中使用的是蒙特卡洛采样
  • 但这里没有显式的包含 s ，所以作者利用著名的jensen不等式(Jensen’s inequality)对目标函数做了转化，得到了目标函数的一个lower bound，如下

    

    这里的 s=s1,...,sC" role="presentation" style="position: relative;">s=s1,...,sC$s=s_1,...,s_C$，是时间轴上的重点focus的序列，理论上这种序列共有 LC" role="presentation" style="position: relative;">LC$L^C$个。

    利用这个目标函数代替原始的目标函数log p(y|a)，对模型的参数 W 算gradient。

    

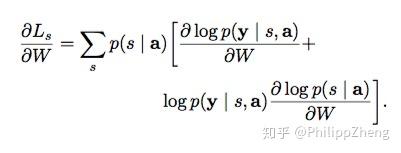
    然后利用蒙特卡洛方法对 s 进行抽样，我们做 N 次这样的抽样实验，记每次取到的序列是 s~n" role="presentation" style="position: relative;">s~n${\tilde{s}}^n$ ，易知 s~n" role="presentation" style="position: relative;">s~n${\tilde{s}}^n$ 的概率为 1N" role="presentation" style="position: relative;">1N$\frac{1}{N}$，所以上面的求gradient的结果即为

    

soft attention

• soft attention每次会照顾到全部的位置，只是不同位置的权重不同。这时 zt" role="presentation" style="position: relative;">zt$z_t$ 即为 ai" role="presentation" style="position: relative;">ai$a_i$ 的加权求和 :

  zt=∑i=1Lαti∗ai" role="presentation" style="position: relative;">zt=∑Li=1αti∗ai$z_t=\sum _{i=1}^L{\alpha }_{ti}\ast a_i$

• 故soft attention是光滑的且可微的（即目标函数，也就是LSTM的目标函数对权重αti" role="presentation" style="position: relative;">αti${\alpha }_{ti}$是可微的，原因很简单，因为目标函数对zt" role="presentation" style="position: relative;">zt$z_t$可微，而zt" role="presentation" style="position: relative;">zt$z_t$ 对 αti" role="presentation" style="position: relative;">αti${\alpha }_{ti}$ 可微，根据chain rule可得目标函数对 αti" role="presentation" style="position: relative;">αti${\alpha }_{ti}$ 可微）。
• 同时可以再做调整，加入βt" role="presentation" style="position: relative;">βt${\beta }_t$：
  • zt=βt∑i=1Lαti∗ai" role="presentation" style="position: relative;">zt=βt∑Li=1αti∗ai$z_t={\beta }_t\sum _{i=1}^L{\alpha }_{ti}\ast a_i$
  • βt=σ(fβ(ht−1))" role="presentation" style="position: relative;">βt=σ(fβ(ht−1))${\beta }_t=\sigma (f_{\beta }(h_{t-1}))$
  • 即根据上一时刻的隐状态决定下一时刻attention相对于ht−1和yt−1" role="presentation" style="position: relative;">ht−1和yt−1$h_{t-1}和y_{t-1}$的比重
• loss function中还加入了αti" role="presentation" style="position: relative;">αti${\alpha }_{ti}$的正则项：

  Ld=−log(P(y|x))+λ∑tC(1−αti)2" role="presentation" style="position: relative;">Ld=−log(P(y|x))+λ∑Ct(1−αti)2$L_d=-log(P(y|x))+\lambda \sum _t^C(1-{\alpha }_{ti}{)}^2$

论文：Effective APProaches to Attention-based Neural Machine Translation

global attention

• 对源语言对所有词进行处理，不同的是在计算attention矩阵值的时候，他提出了几种简单的扩展版本。在他们最后的实验中general的计算方法效果是最好的。
• global attention 在计算context vector ct" role="presentation" style="position: relative;">ct$c_t$ 的时候会考虑encoder所产生的全部hidden state。记decoder时刻 t 的target hidden为 ht" role="presentation" style="position: relative;">ht$h_t$ ，encoder的全部hidden state为h¯s,s=1,2,...,n" role="presentation" style="position: relative;">h¯s,s=1,2,...,n${\overline{h}}_s,s=1,2,...,n$，对于其中任意 h¯s" role="presentation" style="position: relative;">h¯s${\overline{h}}_s$，其权重 αt(s)" role="presentation" style="position: relative;">αt(s)${\alpha }_t(s)$为

  at(s)=align(ht,hs)=exp(score(ht,hs))∑s′exp(score(ht,hs′))" role="presentation">at(s)=align(ht,hs)=exp(score(ht,hs))∑s′exp(score(ht,h′s))$$a_t(s)=align(h_t,h_s)=\frac{exp(score(h_t,h_s))}{\sum _{s^{\prime }}exp(score(h_t,h_s^{\prime }))}$$

  其中，

  

local attention

<\center>

+ 灵感来自于图像中的soft attention和hard attention，soft attention对于源图片中每一小块都进行权重的求和，计算较为费时，而hard attention则计算图像区域 a 在时刻 t 被选中作为输入decoder的信息的概率，有且仅有1个区域被选中，它不可微分，需更加复杂的处理。

+ local attention是一种介于soft和hard之间的方式，使用了一个人工经验设定的参数D去选择一个以pt" role="presentation" style="position: relative;">pt$p_t$为中心，[pt&#x2212;D,pt+D]" role="presentation" style="position: relative;">[pt−D,pt+D]$[p_t-D,p_t+D]$为窗口的区域，进行对应向量的weighted sum，故不像global attention，local alignment vector at" role="presentation" style="position: relative;">at$a_t$的维数是固定的，不随输入序列长度变化而变化，它的维度固定为2D+1

• 此处使用了两种方法去选择pt" role="presentation" style="position: relative;">pt$p_t$：

  • 1.单调对应(Monotonic alignment): 设定pt=t" role="presentation" style="position: relative;">pt=t$p_t=t$
  • 2.Predictive alignment:
    • 使用ht" role="presentation" style="position: relative;">ht$h_t$去预测pt" role="presentation" style="position: relative;">pt$p_t$所在位置：

      S为输入序列长度，此处保证了pt" role="presentation" style="position: relative;">pt$p_t$一定落在输入序列内

      vp&#xFF0C;Wp" role="presentation" style="position: relative;">vp，Wp$v_p，W_p$为权重矩阵

      pt=S&#xA0;&#x2217;sigmoid(vpTtanh(Wpht))" role="presentation" style="position: relative;">pt=S∗sigmoid(vTptanh(Wpht))$p_t=S\ast sigmoid(v_p^{T}tanh(W_p{h}_t))$
• 为了使得最后的求和更加的偏好靠近位置pt" role="presentation" style="position: relative;">pt$p_t$ 附近的向量，又在求和时加入了一个高斯函数，该函数u =pt" role="presentation" style="position: relative;">pt$p_t$,使得pt" role="presentation" style="position: relative;">pt$p_t$周围的向量得到的权重更大，(s即为一般公式中的x，pt" role="presentation" style="position: relative;">pt$p_t$为u，pt" role="presentation" style="position: relative;">pt$p_t$为高斯分布峰值)
  at(s)=align(ht,hs&#x2032;)exp(&#x2212;(s&#x2212;pt)22&#x03C3;2)" role="presentation" style="position: relative;">at(s)=align(ht,h′s)exp(−(s−pt)22σ2)$a_t(s)=align(h_t,h_s^{\prime })exp(-\frac{(s-p_t{)}^2}{2{\sigma }^2})$

  此处依据经验&#x03C3;=D2" role="presentation" style="position: relative;">σ=D2$\sigma =\frac{D}{2}$

结果比较

论文结果中，dot对于global更好，general对于local更好，-m表示Monotonic alignment，-p表示Predictive alignment

self attention

论文：attention is all you need

+ 作者首先指出，结合了RNN(及其变体)和注意力机制的模型在序列建模领域取得了不错的成绩，但由于RNN的循环特性导致其不利于并行计算，所以模型的训练时间往往较长，在GPU上一个大一点的seq2seq模型通常要跑上几天，所以作者对RNN深恶痛绝，遂决定舍弃RNN，只用注意力模型来进行序列的建模。

+ 作者提出一种新型的网络结构，并起了个名字 Transformer，里面所包含的注意力机制称之为 self-attention。作者骄傲地宣称他这套Transformer是能够计算input和output的representation而不借助RNN的唯一的model，所以作者说有attention就够了

+ 从图中可以看出，模型共包含三个attention成分，分别是encoder的self-attention，decoder的self-attention，以及连接encoder和decoder的attention。

这三个attention block都是multi-head attention的形式，输入都是query Q 、key K 、value V 三个元素，只是 Q 、 K 、 V 的取值不同罢了。

scaled Dot-Product Attention

• 文章提出的attention中又称为Scaled Dot-Product Attention

  

  • 对于query Q 、key K 、value V：

    Attention(Q,K,V)=softmax(QKTdk)V" role="presentation" style="position: relative;">Attention(Q,K,V)=softmax(QKTdk√)V$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$

    其中的dk" role="presentation" style="position: relative;">dk$d_k$作为归一化

  • 在传统的 seq2seq 中的 encoder 阶段，我们得到 n 个时刻的 hidden states 之后，可以用每一时刻的 hidden state hi，去分别和任意的 hidden state hj,j=1,2,…,n 计算 attention，这就有点 self-attention 的意思。

    回到当前的模型，由于抛弃了 RNN，encoder 过程就没了 hidden states，那拿什么做 self-attention 呢？

  • 可以想到，假如作为 input 的 sequence 共有 n 个 word，那么我可以先对每一个 word 做 embedding 吧？就得到 n 个 embedding，然后我就可以用 embedding 代替 hidden state 来做 self-attention 了。所以 Q 这个矩阵里面装的就是全部的 word embedding，K、V 也是一样。
  • 所以为什么管 Q 叫query？就是你每次拿一个 word embedding，去“查询”其和任意的 word embedding 的 match 程度（也就是 attention 的大小），你一共要做 n 轮这样的操作。

    我们记 word embedding 的 dimension 为 dmodel ，所以 Q 的 shape 就是 n*dmodel， K、V 也是一样，第 i 个 word 的 embedding 为 vi，所以该 word 的 attention 应为：

    

    那同时做全部 word 的 attention，则是：

    

multi-head attention

• 基于 RNN 的传统 encoder 在每个时刻会有输入和输出，而现在 encoder 由于抛弃了 RNN 序列模型，所以可以一下子把序列的全部内容输进去，来一次 self-attention 。

  理解了 scaled dot-product attention 之后，multi-head attention 就好理解了，因为就是 scaled dot-product attention 的 stacking。

  • 就是把 Q,K,V 通过参数矩阵映射一下，然后再做 Attention，把这个过程重复做 h 次，结果拼接起来就行了，可谓“大道至简”了。具体来说：
  • 

    这里WiQ,WiK,WiV&#x2208;Rdmodel&#x00D7;dk" role="presentation" style="position: relative;">WQi,WKi,WVi∈Rdmodel×dk$W_i^Q,W_i^K,W_i^V\in R^{d_{model}\times d_k}$

  • 然后：

    最后得到一个 n×(hd̃v) 的序列。所谓“多头”（Multi-Head），就是只多做几次同样的事情（参数不共享），然后把结果拼接。

  • 这里如果要生成h个平行的attention，则dk=dmodel/h" role="presentation" style="position: relative;">dk=dmodel/h$d_k=d_{model}/h$，通过头部维度减少，使得其运算代价仍和单头差不多。

attention在CNN中的使用

• 传统的CNN在构建句对模型时如上图，通过每个单通道处理一个句子，然后学习句子表达，最后一起输入到分类器中。这样的模型在输入分类器前句对间是没有相互联系的，作者们就想通过设计attention机制将不同cnn通道的句对联系起来。
• 这篇文章介绍的是利用带注意力机制的卷积神经网络进行句子对建模。句子对建模是自然语言处理中的一个经典问题，在诸如答案选择（Answer Selection, AS）、 释义鉴定（Paraphrase Identification, PI）、文本继承（Textual Entailment, TE）等场景中都有应用。
  • 之前的相关工作多局限于：
    • (1) 设计针对特定场景的特定系统；
    • (2) 对每个句子分开考虑，很少考虑句子之间的影响；
    • (3) 依赖人工设计的繁杂特征。
  • 该模型主要贡献有：
    • (1) 可以应对多种场景的句子对建模问题，泛化能力强；
    • (2) 利用注意力机制，在建模时考虑句子之间的影响；

1.注意力机制

该论文提出了三种注意力机制

1.1 ABCNN-1

两个句子的向量表示s0,s1" role="presentation" style="position: relative;">s0,s1$s_0,s_1$进行match生成attention矩阵，在卷积之前，加入attention矩阵，与表示矩阵s一起进行训练。

1.2 ABCNN-2

在卷积后，对于卷积完成的两个矩阵，进行match，match后按照行和列的求和生成两个矩阵各自的权重，再使用权重对其进行卷积

1.3 ABCNN-3

对于1和2的共同使用

2.效果（3>2>1）

本文提出了三种用于卷积神经网络的注意力机制来进行句子对建模，并在三个常见任务上达到了较好的效果，体现了方法的泛化能力。同时也作者也指出，在三个任务上，两层注意力网络并不会明显优于一层注意力网络，可能是由于相关数据集较小的原因。总的来说，在自然语言处理的相关任务上，卷积神经网络上的注意力机制研究相比长短时记忆网络（LSTM）来说还相对较少，本文是一个较为不错的实现方式。

相关阅读

新型勒索病毒Attention感染医疗与半导体行业

近日,深信服安全团队检测到一种全新的勒索病毒正在活跃,攻击者针对制造行业、医疗行业等目标,通过社会工程、RDP远程爆破等方式手

深度学习中的Attention模型介绍及其进展（attention入门

1. 基本原理   Attention模型最初应用于图像识别，模仿人看图像时，目光的焦点在不同的物体上移动。当神经网络对图像或语言进行识

Attention机制的小理解

1.传统的encode-decode模型 输入序列： 输出序列： 中间语义变量 所以对于，也就是         这就表明输入序列的每一个元素对于输