混淆矩阵
摘要:不用千字,带您透析混淆矩阵。

混淆矩阵(confusion matrix)衡量的是一个分类器分类的准确程度。理解其概念本身容易理解,但一些特定术语易被混淆。
混淆矩阵适用于包含多个分类器的问题,本文为了让读者理解更加容易,以二元分类的混淆矩阵为例进行讲解。
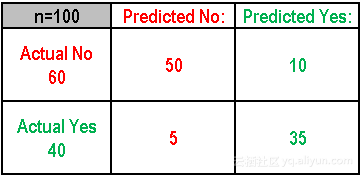
观察混淆矩阵,可得如下结论:
- 示例是一个二元分类问题,产生两种可能的分类:“是”或者“不是”。当预测一个事件是否发生时,“是”意味着该事件已经发生,而“否”则相反,该事件没有发生。
- 该模型对这个事件进行了100次预测。
- 在这100次预测结果中,“是”有45次,“否”有55次。但实际上该事件发生了40次。
重要概念:
- 真阳性(True Positive,TP):样本的真实类别是正例,并且模型预测的结果也是正例
- 真阴性(True Negative,TN):样本的真实类别是负例,并且模型将其预测成为负例
- 假阳性(False Positive,FP):样本的真实类别是负例,但是模型将其预测成为正例
- 假阴性(False Negative,FN):样本的真实类别是正例,但是模型将其预测成为负例
混淆矩阵延伸出的各个评价指标
1.正确率(Accuracy):被正确分类的样本比例或数量
(TP+TN)/Total = (35+50)/100 = 85%
2.错误率(Misclassification/ERROR Rate):被错误分类的样本比例或数量
(FP+FN)/Total = (5+10)/100 = 15%
3.真阳率(True Positive Rate):分类器预测为正例的样本占实际正例样本数量的比例,也叫敏感度(sensitivity)或召回率(recall),描述了分类器对正例类别的敏感程度。
TP/ actual yes = 35/40 = 87%
4.假阳率(False Positive Rate):分类器预测为正例的样本占实际负例样本数量的比例。
FP/actual no = 10/60 = 17%
5.特异性(Specificity):实例是负例,分类器预测结果的类别也是负例的比例。
TN/actual no = 50/60 = 83%
6. 精度(Precision):在所有判别为正例的结果中,真正正例所占的比例。
TP/predicted yes = 35/45 = 77%
7.流行程度(Prevalence):正例在样本中所占比例。
Actual Yes/Total = 40/100 = 40%
关键术语:
- 阳性预测值:其术语概念与精度非常类似,只是在计算阳性预测值考虑了流行程度。在流行程度为50%的时候,阳性预测值(PPV)与精度相同。
- 空错误率:当模型总是预测比例较高的类别,其预测错误的实例所占百分比。在上述示例中,空错误率为60/100 = 60%,因为如果分类器总是预测“是”,那么对于60个为“否”的事件则可能进行错误预测。该指标可用于分类器间的性能比较。然而,对于某些特定的应用程序来说,其最佳分类器的错误率有时会比空错误率更高。
- F值:F 值即为正确率和召回率的调和平均值。
- Roc曲线:即接收者操作特征曲线(receiver operating characteristic curve),反映了真阳性率(灵敏度)和假阳性率(1-特异度)之间的变化关系。Roc曲线越趋近于左上角,预测结果越准确。
译文链接
文章原标题《understanding the Confusion Matrix》
作者:Sunil KAPPal,译者:Elaine,审校:袁虎。
相关阅读
题记: 都说混淆矩阵易混淆,哈哈,下面就来试着尝试一下,看能不能帮助你更好的理解混淆矩阵,以及 AUC 大法。问题:AUC是什么AUC能拿来干什
在机器学习中,当我们使用预先分配好的训练集训练好一个模型后,此时我们会使用预先分配好的测试集来检测我们训练好的这个模型怎么样
4.4.2分类模型评判指标(一) - 混淆矩阵(Confusion Matri
简介 混淆矩阵是ROC曲线绘制的基础,同时它也是衡量分类型模型准确度中最基本,最直观,计算最简单的方法。 一句话解释版本: 混淆矩阵