卷地风来忽吹散
在前面的章节中,我们简要地介绍了卷积神经网络的来龙去脉。接下来我们逐一来解释它之所以成功的几个核心要素。卷积神经网络的名字就来自于其中的卷积操作。因此说到卷积神经网络,它最核心概念可能莫过于“什么是卷积”?
10.1 卷积的数学定义
脱离卷积神经网络这个应用背景,“卷积”其实是一个标准的数学概念。早在3.4节中,我们已经提及到“卷积”的概念:所谓卷积,不过是一个函数和另一个函数在某个维度上的加权“叠加”作用而已[1]。为了更好地理解卷积操作的数学意义,下面我们列举一个具体的案例来加以说明[2]。
假设我们的任务是实时监控一艘宇宙飞船。这艘宇宙飞船带有激光发射器。激光发射器在任意时刻t 都实时输出信号 f(t) ,这里 f(t) 表示飞船在任意时刻 t 所处的位置。通常来说,激光信号中都会夹杂有一定的噪音信号 g(t) 。为了能更加准确地测量飞船的位置,就需要减少噪音的影响,因此我们就需要对获取的距离信号x(t)进行平滑处理。
很显然,对于相邻时间的输出结果,距离当前时间较近的输出,它们对结果的输出影响也较大(分配较大的权值)。反之,距离当前时间越远,它们对当前结果的影响也就越小(分配较小的权值)。因此,加权平均后的飞船位置s(t) 可以用如公式(10.1)表示:

这样的操作就被称为连续域上的卷积操作。这种操作通常也简单记为公式(10.2):

在公式(10.2)中,通常把函数f称为输入函数, g 称为滤波器或卷积核(kernel),这两个函数的叠加结果称为特征图或特征图谱(feature map)
在理论上,输入函数可以是连续的,因此通过积分可以得到一个连续的卷积。但实际上,目前基本上所有计算机都是数字计算机,这样的计算机是不能处理连续(模拟)信号的。因此需要把连续函数离散化。
一般情况下,我们并不需要记录任意时刻的数据,而是以一定的时间间隔(也即频率)采样即可。这么说是有理论根据的,根据香农采样定理,当采样频率应不小于模拟信号频谱中最高频率的2倍时,可以不失真地恢复模拟信号。对于离散信号,卷积操作可用如公式(10.3)表示:
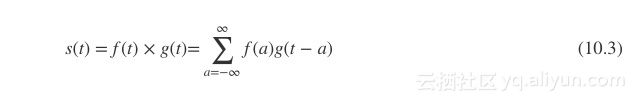
当然,对于离散卷积的定义推广到更高维度的空间上。例如二维的公式可表示为公式(10.4)所示:
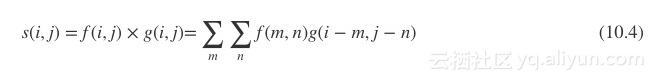
10.2生活中的卷积
卷积的概念好像比较抽象。好在理论来源于现实的归纳和抽象。为了便于理解这个概念,我们可以借助现实生活中案例,来反向演绎说明这个概念。
在前面章节的描述中,我们已经提到,函数(function)就是功能(function),功能就是函数。函数的加权叠加作用,更通俗点讲,就是功能的叠加作用。如果是函数是抽象的,那么功能则是具体的。我们很容易从生活中找到“卷积”影子,从而能更加形象地解释这个概念。在这方面,李德毅院士是高手。
在2015中国计算机大会特邀报告上,笔者有幸聆听了中国人工智能学会理事长李德毅院士的主题报告。在报告中,李院士便提到了卷积的理解问题,非常有意思[3]。
他讲到,什么叫卷积呢?举例来说,在一根铁丝某处不停地弯曲,假设发热函数是f(t) ,散热函数是 g(t) ,此时此刻的温度就是 f(t) 跟g(t)的卷积。在一个特定环境下,发声体的声源函数是f(t) ,该环境下对声源的反射效应函数是 g(t) ,那么这个环境下的接受到声音就是 f(t) 和 g(t) 的卷积。
类似地,记忆其实也是一种卷积的结果。假设认知函数是 f(t) ,它代表对已有事物的理解和消化,随时间流逝而产生的遗忘函数是g(t),那么人脑中记忆函数 h(t) 就是函数是 f(t) 跟g(t) 的卷积,可用如下公式表示。
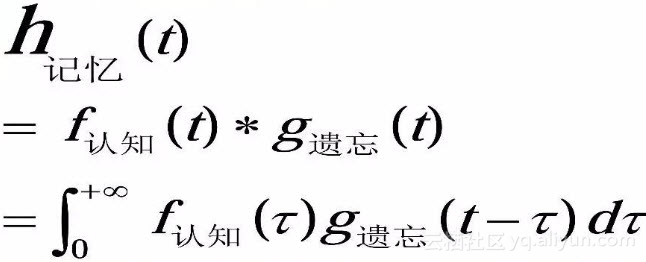
最后,李院士讲到,我们计算机工作者要了解卷积,就要了解卷积神经网络。这个观点和今天讲到的主题很应景,下面我们就言归正“卷”,接着聊卷积神经网络。
10.3在图像处理中的卷积
图像识别是卷积神经网络发威的“圣地”。所以下面我们就以图像处理为例,来说明卷积的作用。
对于如图10-1所示的左侧的图像,正常人很容易判定出,图像中分别是一个数字“8”和一只猫。但是,对于计算机而言,它们看到数字矩阵(每个元素都是0到255之间像素值),至于它们据此能不能判定出是数字“8”和猫,这要依赖于计算机算法,这也是人工智能的研究方向。

图10-1 计算机“眼中”的图像
在如图10-1所示的矩阵中,每个元素表示的都是像素的亮度强度。在这里,0表示黑色,255表示白色,数字越小,越接近黑色。在灰度图像中,每个像素值仅表示一种颜色的强度。也就是说,它只有一个通道。而在彩像中,可以有3个通道,即RGB(红,绿,蓝)。在这种情况下,把三个不同通道的像素矩阵堆叠在一起,即可描述彩色图像。
在图像处理中应用卷积操作,主要目的就是从图像中提取特征。卷积可以很方便地通过从输入的一小块数据矩阵(也就是一小块图像)中学到图像的特征,并能保留像素间的空间关系。下面举例说明在二维图像使用卷积过程。
在图10-2中,为了便于读者理解,图像数据矩阵的像素值分别用诸如a-b-c-d这样的字母代替,卷积核是一个2×2的小矩阵。需要注意的是,在其他场合,这个小矩阵,也被称为“滤波器(filter)”或“特征检测器(feature detector)”。
如果把卷积核应用到输入图像的数据矩阵上,依次按照从左到右、从上到下的顺序分别执行卷积运算,就可以得到这个图像的特征图谱(feature map)。在不同的学术论文中,这个术语特征图谱也被称呼为做“卷积特征(convolved feature)”或 “激活图(activation map)”。
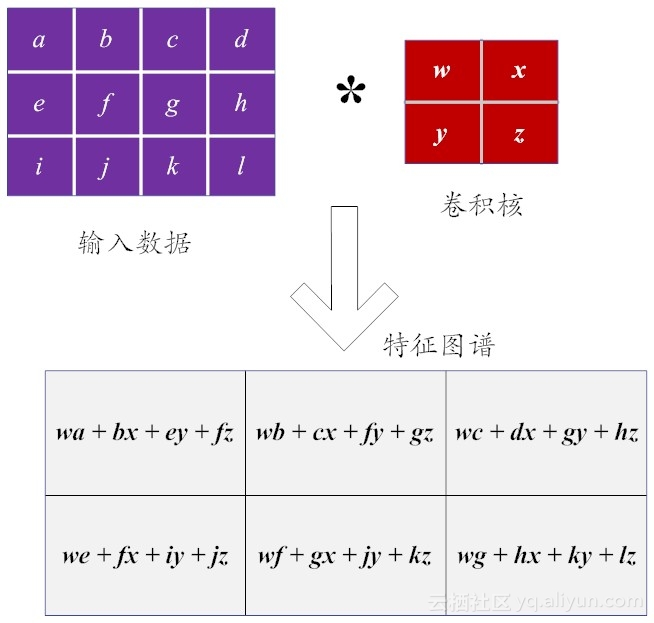
图10-2 二维图像数据上的卷积操作实例
从图10-2体现出来的计算可以看到,在本质上,离散卷积就是一个线性运算。因此,这样的卷积操作也被称为线性滤波。这里的“线性”是指,我们用每个像素的邻域的线性组合来代替这个像素。其实,卷积操作还具有平移不变性(shift-invariant)。这个“平移不变性”是指,在图像的每个位置都执行相同的操作。
这个过程好像并不容易理解,下面我们就用更为浅显易懂的动态图来说明这个卷积过程。正如前文所说,每张图片都可视为关于像素值的数字矩阵。对于灰度图像而言,像素值的范围是0 ~255。为了简单起见,我们考虑一个给定5×5 的极简图像,其像素值仅为或0 或 1。类似地,卷积核是一个3×3的极简矩阵,如图10-3所示。
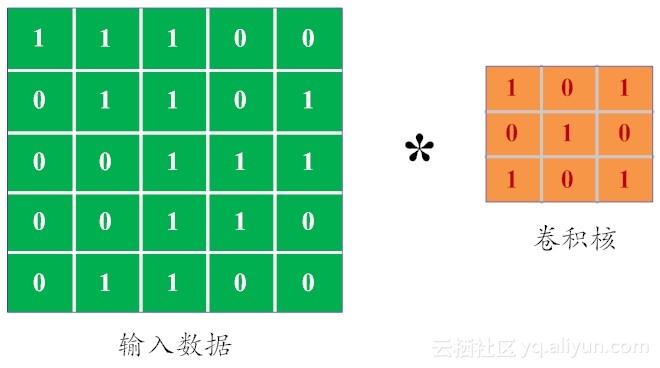
图10-3 简化版本的图像矩阵核卷积核
下面我们来卷积计算是怎么完成的。我们用橙色的矩阵在原始图像(绿色所示矩阵)上从左到右、从上到下滑动,每次滑动一个像素,滑动的距离称为“步幅(stride)”。在每个位置上,我们可以计算出两个矩阵间的相应元素乘积,并把点乘结果之和,存储在输出矩阵(粉色所示)中的每一个单元格中,这样就得到了特征图谱(或称为卷积特征)矩阵[5]。
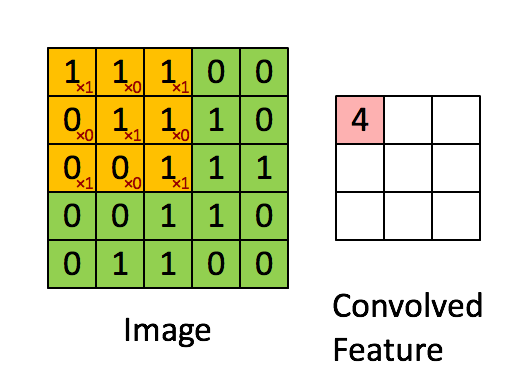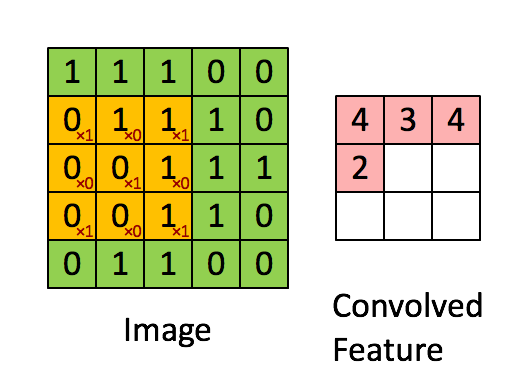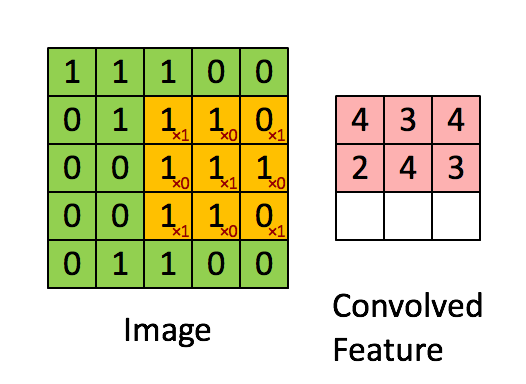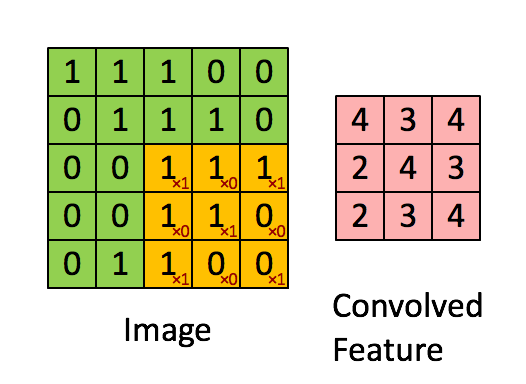
图10-4 卷积的实现过程
10.4卷积在图像处理中的应用
到目前为止,我们只是做了一些简单的矩阵运算而已,它的好处体现在哪里,好像还不十分明确。简单来说,这样做的用途在于,将图像相邻子区域的像素值与卷积核执行“卷积”操作,可以获取相邻数据之间的统计关系,从而可挖掘出图像中的某些重要特征。
这样说来,还是非常地抽象,这些特征到底是什么?下面我们还是用几个图像的案例来形象说明这个概念[6],如图10-5所示。
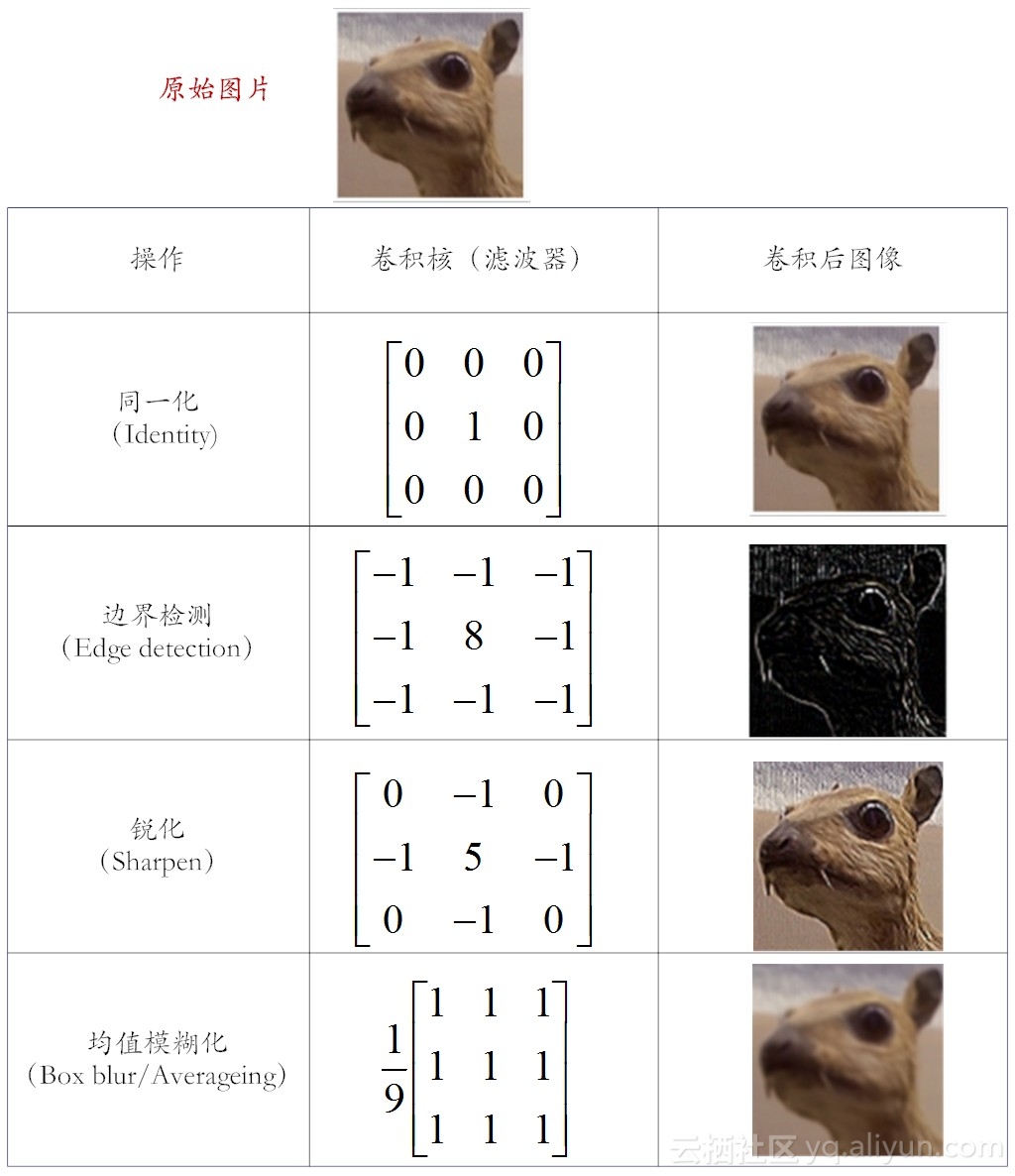
图10-5 “神奇”的卷积核
下面我们简单介绍一下常用的“久经考验”的卷积核。
(1)同一化核(Identity)。从图10-5可见,这个滤波器什么也没有做,卷积后得到的图像和原图一样。因为这个核只有中心点的值是1。邻域点的权值都是0,所以对滤波后的取值没有任何影响。
(2)边缘检测核(Edge Detection),也称为高斯-拉普拉斯算子。需要注意的是,这个核矩阵的元素总和为0(即中间元素为8,而周围8个元素之和为-8),所以滤波后的图像会很暗,而只有边缘位置是有亮度的。
(3)图像锐化核(Sharpness Filter)。图像的锐化和边缘检测比较相似。首先找到边缘,然后再把边缘加到原来的图像上面,如此一来,就强化了图像的边缘,使得图像看起来更加锐利。
(4)均值模糊(Box Blur /Averaging)。这个核矩阵的每个元素值都是1,它将当前像素和它的四邻域的像素一起取平均,然后再除以9。均值模糊比较简单,但图像处理得不够平滑。因此,还可以采用高斯模糊核(Gaussian Blur),这个核被广泛用在图像降噪上。
事实上,还有很多有意思的卷积核,比如说浮雕核(embossing Filter),它可以给图像营造一种比较艺术化的3D阴影效果,如图10-6所示。浮雕核将中心一边的像素值减去另一边的像素值。这时,卷积出来的像素值可能是负数,我们可以将负数当成阴影,而把正数当成光,然后再对结果图像加上一定数值的偏移即可。

图10-6 浮雕核的应用
10.5 小结
现在我们小结一下本章的内容,我们首先给出了卷积的数学定义,接着用生活中的相近的案例来反向演绎解释了这个概念。最后我们用几个著名的卷积核演示了卷积在图像处理中的应用。
在后面的章节中,我们将详细介绍卷积神经网络的重要结构,包括卷积层(Convolutional Layer)、激活层(Activation Layer,涉及到ReLU的概念)、池化层(Pooling Layer)及全连接层(Full Connected Layer)。
请你关注。
10.6 请你思考
通过前面的学习,请你思考如下问题:
(1)我们常说的分布式特征表示,在卷积神经网络中是如何体现的?
(2)除了本文中描述的常见卷积核,你还知道哪些常用于图像处理的卷积核?
(3)现在非常流行计算机来作画,不论是谷歌团队的inceptionism(“盗梦主义”[7]),还是David Aslan正在使用的“深度风格(Deep Style)”[8](如图10-7所示),都是一种基于神经网络的艺术画风。你知道他们都使用了什么样的卷积核吗?

图10-7 深度风格的画风
参考文献
[1] 张玉宏.云栖社区. 神经网络不胜语, M-P模型似可寻(深度学习入门系列之三)
[2]黄安埠. 深入浅出深度学习.中国工信出版社.2017.6
[3] 李德毅.从脑认知到人工智能.中国计算机大会.2015.10
[4] Savan Visalpara. How do computers see an image ?
[5] Feature extraction using convolution
[6] Ujjwal Karn. An Intuitive Explanation of Convolutional Neural Networks
[7] Alexander Mordvintsev, Christopher Olah, Mike Tyka.
Inceptionism: Going Deeper into Neural Networks.
[8] David Aslan. How Artists Can Use Neural Networks to Make Art
本文节选自《深度学习之美》一书,电子工业出版社2018年7月出版
相关阅读
转载:https://blog.csdn.net/qq_34447388/article/details/78997339 第1章介绍 1. 为什么要进行视频压缩? 未经压缩的数字视频的数
本文转自:汇川技术小型PLC梯形图编程系列教程(零):梯形图编程学习指南http://www.yanjuntech.cn/archives/1969 本人目前接触的都
最近由于工作内容的原因,开始了STM32的学习之旅,现记录下学习的过程,为以后回顾做参考。 经看了很多单片机的学习路径,都一致认为在具
遗传算法简介 遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模
原文地址::http://blog.eeecontrol.com/LabVIEW1/《基于实践的LabVIEW零基础入门视频教程》资料不在多,而在于精,资料太多,反而会